পৃষ্ঠাটি লোড হচ্ছে . . .
দয়াকরে অপেক্ষা করুন।
"লোডিং সময়" আপনার ইন্টারনেট স্পিড এর উপর নির্ভরশীল।
পৃষ্ঠাটি লোড হচ্ছে . . .
দয়াকরে অপেক্ষা করুন।
"লোডিং সময়" আপনার ইন্টারনেট স্পিড এর উপর নির্ভরশীল।
প্রশ্ন: ১ + ৫ + ৯ + ----------------+ ৮১ = ? ৩৬তম বিসিএস
| (ক) ৭৬১ | (খ) ৯৬১ |
| (গ) ৮৬১ | (ঘ) ৬৬১ |
উত্তর: ৮৬১
n তম পদ = a + (n - 1)d অর্থাৎ 81 = 1 + 4n - 4 বা, 4n - 3 = 81 বা,n = 21 সমষ্টি = (শেষপদ + প্রথমপদ)/২ * পদসংখ্যা = (81 + 1)/2 * 21 = 861
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: প্রশ্নবোধক স্থানে কি হবে ? ৩৬তম বিসিএস
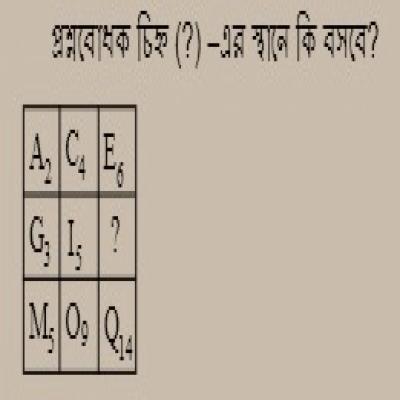
| (ক) \(L_{10}\) | (খ) \(K_{8}\) |
| (গ) \(K_{15}\) | (ঘ) \(L_{15}\) |
উত্তর: \(K_{8}\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: যদি, ৫+৩ = ২৮, ৯+১ = ৮১০, ২+১ = ১৩ হয় তবে, ৫+৪ = ? ৩৬তম বিসিএস
| (ক) ১৮ | (খ) ১৯ |
| (গ) ২১ | (ঘ) ২০ |
উত্তর: ১৯
অঙ্কদ্বয়ের যোগফলের প্রথম অঙ্কটি হবে অঙ্ক বিয়োগফল এবং দ্বিতীয় অঙ্কটি হবে অঙ্কদ্বয়ের যোগফল ৫ - ৩ = ২ এবং ৫ + ৩ = ৮ অতএব ৫ - ৪ = ১ এবং ৫ + ৪ = ৯ অতএব সংখ্যাটি ১৯
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: ইংরেজি বর্ণমালার ধারাবাহিকভাবে ১৮ তম অক্ষরের বামদিকে ১০ম অক্ষর কোনটি? ৩৬তম বিসিএস
| (ক) J | (খ) H |
| (গ) S | (ঘ) F |
উত্তর: H
A B C D E F G
\(H_{10}\)
I J K L M N O P Q
\(R_{10}\)
S T অতএব অক্ষটি হবে H
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(\sqrt{১৫.৬০২৫}\) = কত? ৩৬তম বিসিএস
| (ক) ৩.৯৫ | (খ) ৩.৭৫ |
| (গ) ৩.৮৫ | (ঘ) ৩.৬৫ |
উত্তর: ৩.৯৫
\(4.0\) এর বর্গ = \(16.00\)\(15.6025\) যেহেতু \(16\) থেকে সামান্য কম, তাই উত্তরটি \(4\) থেকে সামান্য কম অর্থাৎ \(3.9\) বা \(3.95\) এর ঘরেই হবে। পরীক্ষায় সময় বাঁচাতে এই 'Estimation' বা কাছাকাছি পূর্ণবর্গ সংখ্যা দিয়ে তুলনা করাই সবচেয়ে
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: ৩, ৭, ১৪, ৫, ২১, ৬ ধারার অস্টম সংখ্যাটি কত হবে? ৩৬তম বিসিএস
| (ক) ২৯ | (খ) ৬ |
| (গ) ৭ | (ঘ) ২৮ |
উত্তর: ২৮
এখানে, দুটি ধারা বিদ্যমান । প্রথমটি : ৩ ৪ ৫ ৬ দ্বিতীয়টি : ৭ ১৪ ২১ ২৮ অতএব অষ্টম সংখ্যাটি হবে ২৮
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: চিত্র েথকে কোনটি সঠিক ? ৩৬তম বিসিএস

| (ক) ১০ কেজি | (খ) ৮ কেজি |
| (গ) ৬ কেজি | (ঘ) ৪ কেজি |
উত্তর: ৮ কেজি
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: 261 টি আম তিন ভাইয়ের মধ্যে \(\frac{1}{3}\) : \(\frac{1}{5}\) : \(\frac{1}{9}\) অনুপাতে ভাগ করে দিলে প্রথম ভাই কতটি আম পাবে? ৩৭তম বিসিএস
| (ক) 45 | (খ) 90 |
| (গ) 81 | (ঘ) 135 |
উত্তর: 135
ভাইদের মধ্যে আমগুলোর অনুপাত = 13:15:19 = (13×45):(15×45):(19×45) = 15:9:5 অনুপাতের রাশিগুলোর যোগফল = (15 + 9 + 5) = 29 অতএব প্রথম ভাই আম পাবে (261এর 15/29) টি = 135 টি
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: 10% মুনাফায় 3000 টাকা এবং 8% মুনাফায় 2000 টাকা বিনিয়োগ করলে মোট মূলধনের উপরে গড়ে শতকরা কত হারে মুনাফা পাওয়া যাবে? ৩৭তম বিসিএস
| (ক) 8% | (খ) 9% |
| (গ) 9.2% | (ঘ) 8.2% |
উত্তর: 9.2%
I₁ = p₁n₁r₁ = (3000×1×10)/100 = 300 টাকা
I₂ = P₂n₂r₂ = (2000×1×8)/100 = 160 টাকা
মোট মুনাফা (300+160) = 460 টাকা
মোট মূলধন (3000+2000) = 5000 টাকা
অতএব ,মোট মূলধনের উপর মুনাফার হার = (460×100)/5000% = 9.2%
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: 100 টাকায় 10 টি ডিম কিনে 100 টাকায় 8 টি ডিম বিক্রয় করলে শতকরা লাভ কত হবে? ৩৭তম বিসিএস
| (ক) 16% | (খ) 20% |
| (গ) 25% | (ঘ) 28% |
উত্তর: 25%
1 টি ডিমের ক্রয়মূল্য (১০০/১০) টাকা = ১০ টাকা
1 টি ডিমের বিক্রয়মূল্য (১০০/৮) টাকা = ১২.৫ টাকা
লাভের পরিমাণ = (১২.৫ - ১০) টাকা = ২.৫ টাকা
অতএব লাভের হার = (২.৫*১০০)/১০
= 25%
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(x^{2}-3x+1\) = 0 হলে \(x^{2}-\frac{1}{x^{2}}\) এর মান- ৩৭তম বিসিএস
| (ক) 4√5 | (খ) 6√5 |
| (গ) 3√5 | (ঘ) 5√3 |
উত্তর: 3√5
\(x^{2}-kx+1=0\) আকারে কোনো সমীকরণ থাকলে \(x^{2}-\frac{1}{x^{2}}\) এর মান বের করার দ্রুততম শর্টকাট পদ্ধতি নিচে দেওয়া হলো: Shortcut Formula: যদি \(x^{2}-kx+1=0\) হয়, তবে:\(x^{2}-\frac{1}{x^{2}}=\pm k\sqrt{k^{2}-4}\)এই অংকের ক্ষেত্রে প্রয়োগ (এখানে \(k=3\)): ১. সরাসরি সূত্রে মান বসান: \(3\sqrt{3^{2}-4}\)২. হিসাব করুন: \(3\sqrt{9-4}=3\sqrt{5}\)৩. উত্তর হবে: \(\pm 3\sqrt{5}\) ধাপে ধাপে দ্রুত করার কৌশল (Mental Math): পরীক্ষার হলে মাত্র ৫ সেকেন্ডে করার জন্য এই ধাপগুলো মনে রাখুন: মান বের করা: সমীকরণের মাঝখানের সংখ্যাটিই হলো \((x+\frac{1}{x})\) এর মান। এখানে সেটি ৩।বিয়োগফল বের করা: \((x+\frac{1}{x})\) এর মানের বর্গ থেকে ৪ বিয়োগ করে রুট করুন।\(3^{2}-4=5\rightarrow \sqrt{5}\)গুণ করা: প্রথম মান (৩) এবং দ্বিতীয় মান (\(\sqrt{5}\)) গুণ করে দিন।ফলাফল: \(3\sqrt{5}\) (চিহ্ন হবে \(\pm \)) আরও একটি উদাহরণ: যদি \(x^{2}-5x+1=0\) হয়: \(k=5\)মান হবে: \(\pm 5\sqrt{5^{2}-4}=\pm 5\sqrt{21}\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: x² - 5x + 6 < 0 হলে- ৩৭তম বিসিএস
| (ক) x < 2 | (খ) 2 < x < 3 |
| (গ) x < 3 | (ঘ) -3 < x < -2 |
উত্তর: 2 < x < 3
x2 -3x-2x+6 <0
= x(x-3) - 2(x-3) <0
= (x-3) (x-2) <0 ------- (1)
এখানে সমীকরণটি সত্য হবে যদি (x-3) ও (x-2) এর একটি ধনাত্মক এবং অন্যটি ঋনাতক হয় ।
=> x>3 হলে, x-3>0 এবং x-2>0
=> 2 <x <3 হলে, x-3 <0 এবং x-2 >0
=> x<2 হলে, x-3<0, এবং x-2<0
তাহলে দেখা যাচ্ছে শুধুমাত্র 2<x<3 হলে,(1)নং সমীকরণটি সত্য বলে প্রমাণিত হয় । তাই উওরঃ 2<x<3
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: দুই অংক বিশিষ্ট একটি সংখ্যা, অংকদ্বয় স্থান বিনিময়ের ফলে ৫৪ বৃদ্ধি পায়। অংক দুইটির যোগফল ১২ হলে সংখ্যাটি কত? ৩৭তম বিসিএস
| (ক) 57 | (খ) 75 |
| (গ) 39 | (ঘ) 93 |
উত্তর: 39
সংখ্যাটি 57 হলে অংকদ্বয় স্থান বিনিময় করার পর হয় 75 এবং পার্থক্য (75 - 57) = 18 সংখ্যাটি 39 হলে অংকদ্বয় স্থান বিনিময় করার পর হয় 93 এবং পার্থক্য (93 - 39) = 54 এবং অংক দুটির যোগফল (9 + 3) = 12 , যা অংকের শর্তকে সিদ্ধ করে। অতএব নির্ণেয় সংখ্যা 39
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(\log _{x}(\frac{3}{2})\) =− \(\frac{1}{2}\) হলে, x এর মান ৩৭তম বিসিএস
| (ক) \(\frac{9}{4}\) | (খ) \(\frac{6}{3}\) |
| (গ) \(\frac{5}{7}\) | (ঘ) \(\frac{4}{9}\) |
উত্তর: \(\frac{4}{9}\)
১. লগারিদমের সংজ্ঞা: \(\log _{x}(\frac{3}{2})=-\frac{1}{2}\) থেকে পাই \(x^{-\frac{1}{2}}=\frac{3}{2}\)।২. ঋণাত্মক ঘাত: \(x^{-\frac{1}{2}}\) মানে হলো \(\frac{1}{x^{1/2}}\) বা \(\frac{1}{\sqrt{x}}\)।৩. আড়গুণন (Cross-multiplication): \(\frac{1}{\sqrt{x}}=\frac{3}{2}\Rightarrow 3\sqrt{x}=2\)।৪. উভয়পক্ষকে বর্গ: \((3\sqrt{x})^{2}=2^{2}\Rightarrow 9x=4\)।৫. চূড়ান্ত মান: \(x=\frac{4}{9}\)।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: একটি সমান্তর অনুক্রমে সাধারণ অন্তর 10 এবং 6-তম পদটি 52 হলে 15-তম পদটি-- ৩৭তম বিসিএস
| (ক) 140 | (খ) 150 |
| (গ) 142 | (ঘ) 148 |
উত্তর: 142
প্রথম পদ a ও সাধারণ অন্তর d হলে। r - তম পদ = a + (r - 1)d অতএব 6 - তম '' a = a + (6 - 1)d = > 52 = a + 5
×
10 = > a = 52 - 50 অতএব a = 2 অতএব 15 - তম পদ = 2 + (15 - 1)
×
10 = 2 + 140 = 142
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।