পৃষ্ঠাটি লোড হচ্ছে . . .
দয়াকরে অপেক্ষা করুন।
"লোডিং সময়" আপনার ইন্টারনেট স্পিড এর উপর নির্ভরশীল।
পৃষ্ঠাটি লোড হচ্ছে . . .
দয়াকরে অপেক্ষা করুন।
"লোডিং সময়" আপনার ইন্টারনেট স্পিড এর উপর নির্ভরশীল।
প্রশ্ন: \(\log _{x}\frac{1}{8}=-2\) হলে \(x\) এর মান ৩৮তম বিসিএস
| (ক) √2 | (খ) 2√2 |
| (গ) 2 | (ঘ) 4 |
উত্তর: 2√2
ধাপ ১: সূচকীয় আকারে রূপান্তর লগারিদমের সূত্রানুসারে, \(\log _{a}b=c\) হলে \(a^{c}=b\) হয়।সেই অনুযায়ী:\(x^{-2}=\frac{1}{8}\)ধাপ ২: \(x\) এর মান নির্ণয় \(\frac{1}{x^{2}}=\frac{1}{8}\)\(x^{2}=8\)\(x=\sqrt{8}\)\(x=\sqrt{4\times 2}\)\(x=2\sqrt{2}\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(2^{x}+2^{1-x}=3\) হলে, x= কত ? ৩৮তম বিসিএস
| (ক) ( 1, 3) | (খ) ( 0, 1) |
| (গ) ( 0, 2 ) | (ঘ) ( 1, 2) |
উত্তর: ( 0, 1)
\(2^{x}+2^{1-x}=3\) এর মতো অংকের জন্য দ্রুত সমাধান করার উপায় হলো শুদ্ধি পরীক্ষা (Option Test)। ১. টেকনিক:যেহেতু সমীকরণের ডানপক্ষ \(3\) (একটি পূর্ণসংখ্যা), তাই \(x\) এর মান এমন হবে যাতে \(2^{x}\) একটি পূর্ণসংখ্যা বা সহজ ভগ্নাংশ হয়। সাধারণত এই ধরণের অংকে \(x\) এর মান \(0,1,2\) বা \(-1\) এর মধ্যেই থাকে। ২. মান বসিয়ে পরীক্ষা: \(x=0\) বসিয়ে: \(2^{0}+2^{1-0}=1+2=3\) (মিলে গেছে)\(x=1\) বসিয়ে: \(2^{1}+2^{1-1}=2+2^{0}=2+1=3\) (মিলে গেছে) ৩. শর্টকাট সূত্র:যদি সমীকরণটি \(a^{x}+\frac{a^{k}}{a^{x}}=a^{k}+1\) আকারে থাকে, তবে উত্তর হয় \(x=0\) এবং \(x=k\)।এখানে \(2^{x}+\frac{2}{2^{x}}=2+1\) আকারে আছে (যেখানে \(k=1\))।সরাসরি উত্তর: \(x=0,1\)।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: বাস্তব সংখ্যায় |2x−3| ≤ অসমতাটির সমাধান-- ৩৮তম বিসিএস
| (ক) x≤ 1 অথবা x≥ 2 | (খ) 1< x <2 |
| (গ) 1≤ x ≤ 2 | (ঘ) −1< x <2 |
উত্তর: 1≤ x ≤ 2
বাস্তব সংখ্যায় \(|2x-3|\le 1\) (সাধারণত এই অংকে মান ১ থাকে) অসমতাটির সমাধান হলো \(\mathbf{1\le x\le 2}\)। এটি একটি পরম মান সংবলিত অসমতা, যার সমাধান নিচে ধাপে ধাপে দেওয়া হলো: ধাপ ১: পরম মান তুলে দেওয়া আমরা জানি, \(|x|\le a\) হলে, \(-a\le x\le a\) হয়।সেই সূত্র অনুযায়ী:\(-1\le 2x-3\le 1\)ধাপ ২: অসমতাটি সমাধান করা অসমতার প্রতিটি অংশের সাথে \(3\) যোগ করে পাই:\(-1+3\le 2x-3+3\le 1+3\)\(2\le 2x\le 4\)এখন, প্রতিটি অংশকে \(2\) দ্বারা ভাগ করে পাই:\(\frac{2}{2}\le \frac{2x}{2}\le \frac{4}{2}\)\(1\le x\le 2\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: একটি সমান্তর অনুক্রমে 5ম পদটি 18 এবং প্রথম 5টি পদের যোগফল 75 হলে প্রথম পদটি কত ? ৩৮তম বিসিএস
| (ক) 10 | (খ) 4 |
| (গ) 12 | (ঘ) 2 |
উত্তর: 12
সমষ্টির সূত্র প্রয়োগ আমরা জানি, সমান্তর ধারার প্রথম \(n\) পদের সমষ্টির সূত্র হলো:\(S_{n}=\frac{n}{2}(a+a_{n})\)এখানে,\(a\) = প্রথম পদ\(n\) = পদের সংখ্যা = 5\(a_{5}\) = 5ম পদ = 18\(S_{5}\) = প্রথম 5টি পদের যোগফল = 75 ধাপ ২: মান বসিয়ে প্রথম পদ (a) নির্ণয় সূত্রে মানগুলো বসিয়ে পাই:\(75=\frac{5}{2}(a+18)\)\(75\times 2=5(a+18)\)\(150=5a+90\)\(5a=150-90\)\(5a=60\)\(a=\frac{60}{5}\)\(a=12\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: একটি সমাবহু ত্রিভুজের একটি বাহুর দৈর্ঘ্য a একক হলে, ত্রিভুজের ক্ষেত্রফল কত বর্গ একক ? ৩৮তম বিসিএস
| (ক) \(\frac{\sqrt{3}}{4}a^{2}\) | (খ) \(\frac{\sqrt{3}}{2}a^{2}\) |
| (গ) \(\frac{\sqrt{4}}{3}a^{2}\) | (ঘ) \(\frac{\sqrt{2}}{3}a^{2}\) |
উত্তর: \(\frac{\sqrt{3}}{4}a^{2}\)
একটি সমবাহু ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যই সমান থাকে। জ্যামিতিক উপায়ে উচ্চতা নির্ণয় করে ক্ষেত্রফল বের করলে এই সূত্রটি পাওয়া যায়: \(=\frac{\sqrt{3}}{4}a^{2}\)এখানে: \(a\): ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য।\(\sqrt{3}\): ৩ এর বর্গমূল (মান প্রায় ১.৭৩২)। উদাহরণ:যদি কোনো সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য \(2\) মিটার হয়, তবে তার ক্ষেত্রফল হবে:\(\frac{\sqrt{3}}{4}\times 2^{2}=\frac{\sqrt{3}}{4}\times 4=\sqrt{3}\) বা প্রায় ১.৭৩২ বর্গমিটার।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: একটি কোনের মান তার পুরক কোনের মানের অর্ধেকের সমান। কোনটির মান কত? ৩৮তম বিসিএস
| (ক) 30° | (খ) 60° |
| (গ) 45° | (ঘ) 25° |
উত্তর: 30°
ধরা যাক, x কোণটির মান।
তাহলে, x এর পূরক কোণের মান হবে (90 - x)°।
প্রশ্ন অনুযায়ী, x = (90 - x) / 2
2x = 90 - x
3x = 90
x = 30°
সুতরাং, কোণটির মান 30°।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: চিত্র থেকে ৩৮তম বিসিএস
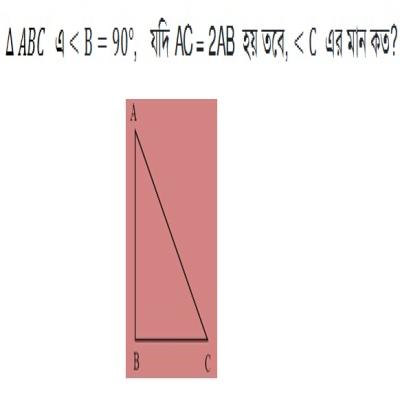
| (ক) 22.5 ডিগ্রী | (খ) 30 ডিগ্রী |
| (গ) 60 ডিগ্রী | (ঘ) 45 ডিগ্রী |
উত্তর: 30 ডিগ্রী
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: একজন লোক একটি নির্দিষ্ট স্থান A থেকে যাত্রা শুরু করে ১২ কি.মি উত্তর দিকে গেলে এবং সেখান থেকে ৫ কি.মি পূর্ব দিকে গেল। যাত্রা শেষে সে A অবস্থান থেকে কত দূরে থাকবে? ৩৮তম বিসিএস
| (ক) ১৩ কি.মি | (খ) ১৫ কি.মি |
| (গ) ১৭ কি.মি | (ঘ) ১৪ কি.মি |
উত্তর: ১৩ কি.মি
ব্যাখাঃ মনে করি, লোকটি A বিন্দু থেকে ১২ কিমি উত্তরে B বিন্দুতে যাওয়ার পর ঠিক পূর্বদিকে ৫ কিমি গিয়ে C বিন্দুতে পৌছায়। এক্ষেত্রে ABC সমকোণী ত্রিভুজ উৎপন্ন করে। সমকোণী ত্রিভুজের বাহুর অনুপাত হচ্ছে ৫ঃ১২ঃ১৩। সুতরাং AC। এর দূরুত্ব হবে ১৩ কিমি।
বি:দ্র: সমকোণী ত্রিভুজ আঁকতে হবে
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(125(\sqrt{5})^{2x}\) =1 হলে x এর মান কত? ৩৯তম বিসিএস (স্বাস্থ্য ক্যাডার)
| (ক) 9 | (খ) 3 |
| (গ) 7 | (ঘ) -3 |
উত্তর: -3
\(125(\sqrt{5})^{2x}=1\) এর জন্য দ্রুত সমাধান করার শর্টকাট উপায়: ১. টেকনিক (ভিত্তি ৫-এ রূপান্তর):সব সংখ্যাকে ৫ এর পাওয়ার হিসেবে চিন্তা করুন। \(125=5^{3}\)\((\sqrt{5})^{2x}=(5^{1/2})^{2x}=5^{x}\)২. সরাসরি যোগফল শূন্য করা:যেহেতু ডানপাশে \(1\) আছে, তাই বামপাশের সকল পাওয়ারের যোগফল ০ (শূন্য) হতে হবে।অর্থাৎ: \(3+x=0\) ৩. মুখে মুখে হিসাব:\(125\) এর জন্য পাওয়া যায় \(3\)\((\sqrt{5})^{2x}\) এর জন্য পাওয়া যায় \(x\)সুতরাং, \(3+x=0\Rightarrow \mathbf{x=-3}\)।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(nC_{12}=nC_{6}\) হলে n এর মান কত? ৩৯তম বিসিএস (স্বাস্থ্য ক্যাডার)
| (ক) 14 | (খ) 18 |
| (গ) 16 | (ঘ) 12 |
উত্তর: 18
আমরা জানি, সমাবেশের সূত্র অনুযায়ী, যদি \(nC_{x}=nC_{y}\) হয়, তবে হয় \(x=y\) হবে অথবা \(\mathbf{n=x+y}\) হবে।এখানে দেওয়া আছে:\(nC_{12}=nC_{6}\)ধাপ ২: \(n\) এর মান নির্ণয় যেহেতু \(\ne \), তাই আমরা দ্বিতীয় শর্তটি ব্যবহার করি:\(n=12+6\)\(n=18\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: যদি ৯×৭=৩৫৪৫ এবং ৪×৩=১৫২০ হয় তবে, ৬×৮=? ৩৯তম বিসিএস (স্বাস্থ্য ক্যাডার)
| (ক) ৪০৩০ | (খ) ৩০৪০ |
| (গ) ৬০৫০ | (ঘ) ৫০৪০ |
উত্তর: ৪০৩০
৯×৫ = ৪৫,৭×৫ = ৩৫→৩৫৪৫;
৪×৫ = ২০ ৩×৫ = ১৫→১৫২০ ৬×৫ = ৩০, ৮×৫ = ৪০→৪০৩০.
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: বার্ষিক শতকরা 10% হারে 1000 টাকার 2 বছর পর সরল ও চক্রবৃদ্ধির মুনাফার পার্থক্য কত? ৩৯তম বিসিএস (স্বাস্থ্য ক্যাডার)
| (ক) 11.5 টাকা | (খ) 10 টাকা |
| (গ) 11 টাকা | (ঘ) 12 টাকা |
উত্তর: 10 টাকা
সরল মুনাফা, I = 1000×2×(10/100) = 200 টাকা
চক্রবৃদ্ধি মুনাফা, Ic = 1000{(1+10/100)^2 -1 }
= 1000(121/100 -1)
= (1000×21)/100 = 210 টাকা
সরল ও চক্রবৃদ্ধি মুনাফার পার্থক্য = (210-200) টাকা
= 10 টাকা
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: দুইটি সংখ্যার অনুপাত 7: 5 এবং তাদের ল.সা.গু 140 হলে সংখ্যা দুইটির গ.সা.গু কত? ৩৯তম বিসিএস (স্বাস্থ্য ক্যাডার)
| (ক) 12 | (খ) 6 |
| (গ) 4 | (ঘ) 9 |
উত্তর: 4
ধরি, সংখ্যা দুটি 7x ও 5x , যেখানে x হলো সংখ্যা দুটির গ.সা.গু
∴ 7x × 5x = 140 × x
= > 35x = 140
= > x = 4
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: 2\({x^2}\)+5\({x}\)+3<0 এর সমাধান কোনটি? ৩৯তম বিসিএস (স্বাস্থ্য ক্যাডার)
| (ক) - \(\frac{3}{2}\) < \({x}\) < -1 | (খ) - \(\frac{3}{2}\) ≤ \({x}\)≤1 |
| (গ) - \(\frac{3}{2}\) < \({x}\) < 1 | (ঘ) - \(\frac{3}{2}\) ≤ \({x}\)≤-1 |
উত্তর: - \(\frac{3}{2}\) < \({x}\) < -1
প্রদত্ত অসমতা: \(2x^{2}+5x+3<0\) ধাপ ১: বামপক্ষকে উৎপাদকে বিশ্লেষণ (Factorization)মধ্যপদ বিভাজন (Middle-term break) পদ্ধতিতে:\(2x^{2}+2x+3x+3<0\)বা, \(2x(x+1)+3(x+1)<0\)বা, \((x+1)(2x+3)<0\) ধাপ ২: ক্রান্তি বিন্দু (Critical points) নির্ণয়অসমতাটিকে শূন্য ধরে পাই:\(x+1=0\Rightarrow x=-1\)\(2x+3=0\Rightarrow x=-3/2\) বা \(-1.5\) ধাপ ৩: সমাধান এলাকা পরীক্ষাযেহেতু গুণফলটি শূন্যের চেয়ে ছোট (ঋণাত্মক), তাই \(x\)-এর মান ছোট বিন্দু \((-1.5)\) থেকে বড় এবং বড় বিন্দু \((-1)\) থেকে ছোট হতে হবে। অর্থাৎ, \(-1.5<x<-1\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: একজন লোক A অবস্থান থেকে হেঁটে ডান দিকে ১০ ফুট, অত:পর বামদিকে ২০ ফুট , তারপর বামদিকে ২০ ফুট এবং সবশেষে বামদিকে ২০ ফুট গিয়ে B অবস্থানে পৌঁছাল। A ও B এর মধ্যকার দূরত্ব কত ফুট? ৩৯তম বিসিএস (স্বাস্থ্য ক্যাডার)
| (ক) ৩০ ফুট | (খ) ১০ ফুট |
| (গ) ৪০ ফুট | (ঘ) ২০ ফুট |
উত্তর: ১০ ফুট
BC = ২০ ফুট ; AC = ১০ ফুট .'. BA = ২০ - ১০ = ১০ ফুট
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।